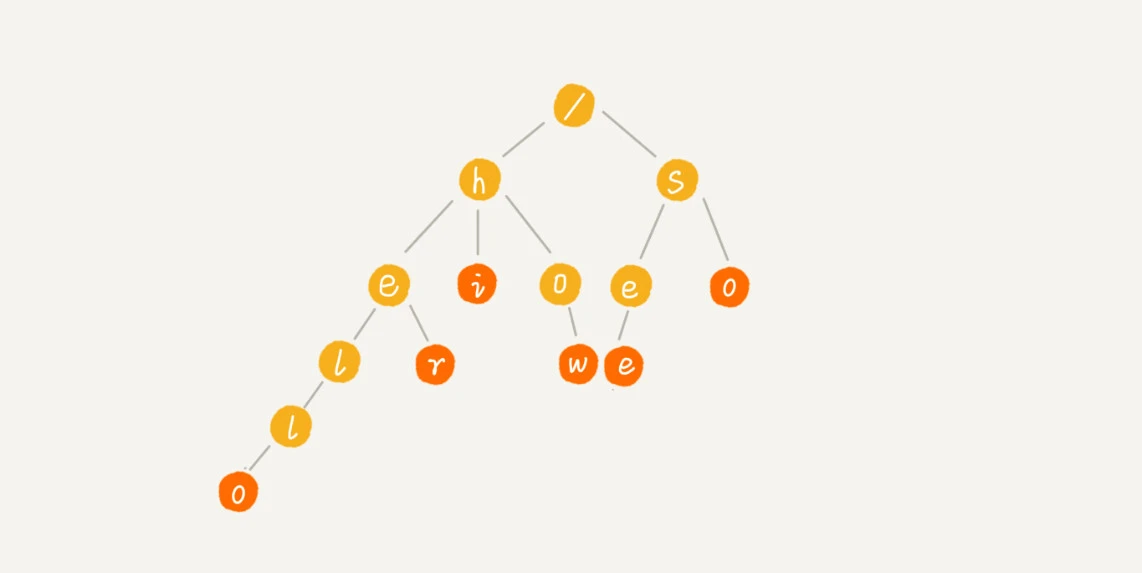
数据结构与算法:Trie树
Trie 树,也叫“字典树”。顾名思义,它是一个树形结构。它是一种专门处理字符串匹配的数据结构,用来解决在一组字符串集合中快速查找某个字符串的问题。它的本质,就是利用字符串之间的公共前缀,将重复的前缀合并在一起。
Trie树的实现
Trie 树主要有两个操作,一个是将字符串集合构造成 Trie 树。这个过程分解开来的话,就是一个将字符串插入到 Trie 树的过程。另一个是在 Trie 树中查询一个字符串。
代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
public class Trie
{
private Node _root;
public Trie()
{
_root = new Node('/');
}
public void insert(string data)
{
var node = _root;
for (int i = 0; i < data.Length; i++)
{
var index = data[i] - 'a';
if (node.SubNodes[index] == default(Node))
{
node.SubNodes[index] = new Node(data[i]);
}
node = node.SubNodes[index];
}
}
public List<string> Match(string pre)
{
if (string.IsNullOrWhiteSpace(pre)) return null;
var node = _root;
for (int i = 0; i < pre.Length; i++)
{
var index = pre[i] - 'a';
node = node.SubNodes[index];
if (node == default(Node))
{
return null;
}
}
return Search(node)?.Select(x => pre + x)?.ToList();
}
private List<string> Search(Node node)
{
var strs = new List<string>();
for (int i = 0; i < 26; i++)
{
if (node.SubNodes[i] == default(Node)) continue;
strs.AddRange(Search(node.SubNodes[i])?.Select(x => node.SubNodes[i].Data + x) ?? new List<string>() { node.SubNodes[i].Data.ToString() });
}
if (strs.Count == 0) return null;
else return strs;
}
class Node
{
public Node(char data)
{
Data = data;
}
public char Data { get; set; }
public Node[] SubNodes { get; set; } = new Node[26];
}
}
内存空间占用问题
如果字符串中包含从 a 到 z 这 26 个字符,那每个节点都要存储一个长度为 26 的数组,并且每个数组元素要存储一个 8 字节指针(或者是 4 字节,这个大小跟 CPU、操作系统、编译器等有关)。而且,即便一个节点只有很少的子节点,远小于 26 个,比如 3、4 个,我们也要维护一个长度为 26 的数组。我们前面讲过,Trie 树的本质是避免重复存储一组字符串的相同前缀子串,但是现在每个字符(对应一个节点)的存储远远大于 1 个字节。按照我们上面举的例子,数组长度为 26,每个元素是 8 字节,那每个节点就会额外需要 26*8=208 个字节。而且这还是只包含 26 个字符的情况。如果字符串中不仅包含小写字母,还包含大写字母、数字、甚至是中文,那需要的存储空间就更多了。所以,也就是说,在某些情况下,Trie 树不一定会节省存储空间。在重复的前缀并不多的情况下,Trie 树不但不能节省内存,还有可能会浪费更多的内存。Trie 树尽管有可能很浪费内存,但是确实非常高效。那为了解决这个内存问题,我们可以稍微牺牲一点查询的效率,将每个节点中的数组换成其他数据结构,来存储一个节点的子节点指针。用哪种数据结构呢?我们的选择其实有很多,比如有序数组、跳表、散列表、红黑树等。
Trie 树与散列表、红黑树的比较
字符串中包含的字符集不能太大。我们前面讲到,如果字符集太大,那存储空间可能就会浪费很多。即便可以优化,但也要付出牺牲查询、插入效率的代价。 要求字符串的前缀重合比较多,不然空间消耗会变大很多。 如果要用 Trie 树解决问题,那我们就要自己从零开始实现一个 Trie 树,还要保证没有 bug,这个在工程上是将简单问题复杂化,除非必须,一般不建议这样做。 我们知道,通过指针串起来的数据块是不连续的,而 Trie 树中用到了指针,所以,对缓存并不友好,性能上会打个折扣。 Trie树不适合精确匹配查找,这种问题更适合用散列表或者红黑树来解决。Trie 树比较适合的是查找前缀匹配的字符串