数据结构与算法：链表

定义

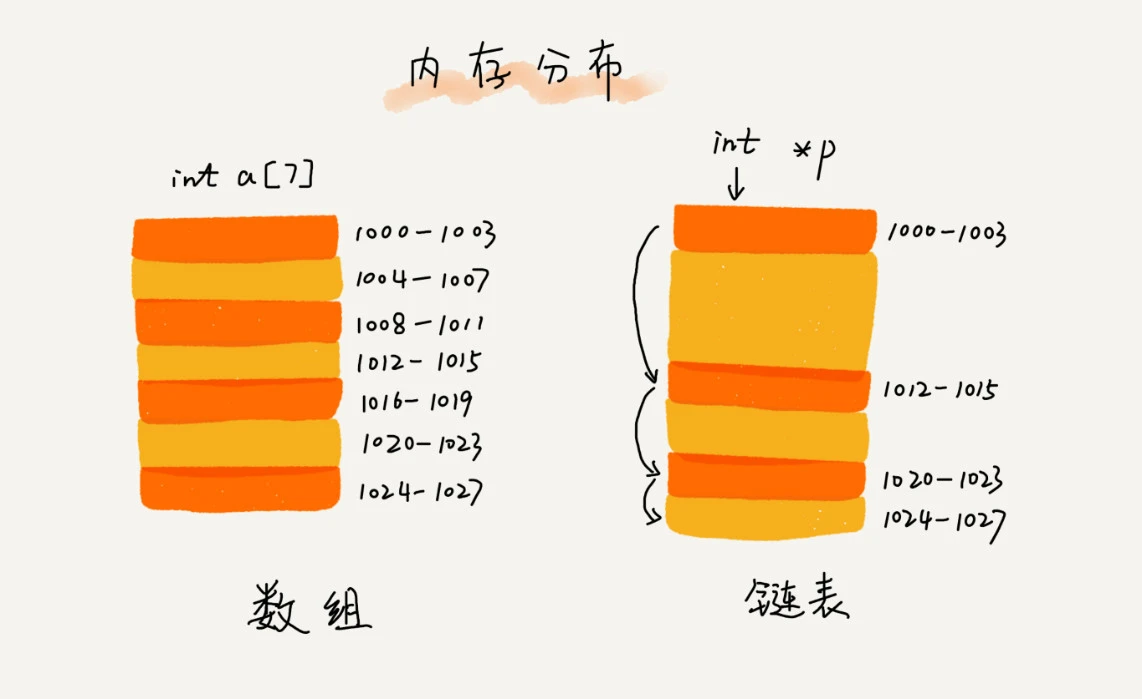
链表由一系列结点（链表中每一个元素称为结点）组成，结点可以在运行时动态生成。每个结点包括两个部分：一个是存储数据元素的数据域，另一个是存储下一个结点地址的指针域。链表是一种物理存储单元上非连续、非顺序的存储结构，数据元素的逻辑顺序是通过链表中的指针链接次序实现的。

链表和数组一样，作为最底层的数据结构，是很多其他数据结构的底层实现，比如可以用链表来实现队列、栈等等。相比数组对连续内存空间的要求限制，链表对内存的使用就更加灵活，它不需要一块连续的内存空间，而是通过指针将一组零散的内存块串联起来。

复杂度分析

• 查询：需要遍历链表，时间复杂度为O(n)
• 删除：因为删除数据前需要遍历链表找到要删除的节点，所以时间复杂度同样为O(n),单纯的删除操作为O(1)
• 插入节点：插入到链尾的时间复杂度为O(1)

常见的链表结构

最常见的三种链表结构分别是：单链表，双向链表，循环链表。

单链表

链表通过指针将一组零散的内存块串联在一起，其中每一个内存块就是链表中的一个节点（node），为了所有节点串联起来，节点中不仅要存储数据（data），还需要存储指向下一个节点地址的指针（*next）。结构如下图：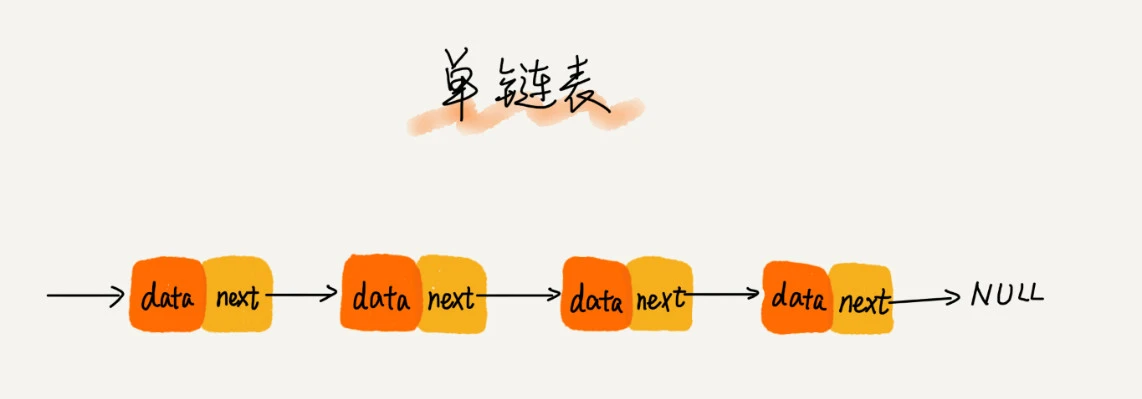

我们习惯把第一个节点成为头节点，最后一个节点称为尾节点。尾节点的next指向null，这样我们就可以通过头节点遍历整条链表，直到尾节点的next为null结束。有序链表代码实现如下：

type LinkList struct {
	head *LinkNode
}

type LinkNode struct {
	data int
	next *LinkNode
}

func (l *LinkList) Insert(data int) {

	if l.head == nil {
		l.head = &LinkNode{
			data: data,
			next: nil,
		}
		return
	}
	t := l.head
	priv := l.head
	i := 0
	for t != nil {
		if i == 0 {
			if data < t.data {
				node := &LinkNode{
					data: data,
					next: t,
				}
				l.head = node
				return
			}
		}
		if data < t.data {
			t2 := priv.next
			priv.next = &LinkNode{
				data: data,
				next: t2,
			}
			return
		}
		priv = t
		t = t.next
		i++
	}
	priv.next = &LinkNode{
		data: data,
		next: nil,
	}
}

func (l *LinkList) Print() {
	n := l.head
	for n != nil {
		fmt.Printf("n.data: %v\n", n.data)
		n = n.next
	}
}

双向链表

双向链表同样是单链表的变式，区别是节点中不仅要存储next指针，还需要存储一个指向上一个节点的指针（*prev），这样就可以实现链表的双向遍历，提高了链表操作的灵活性。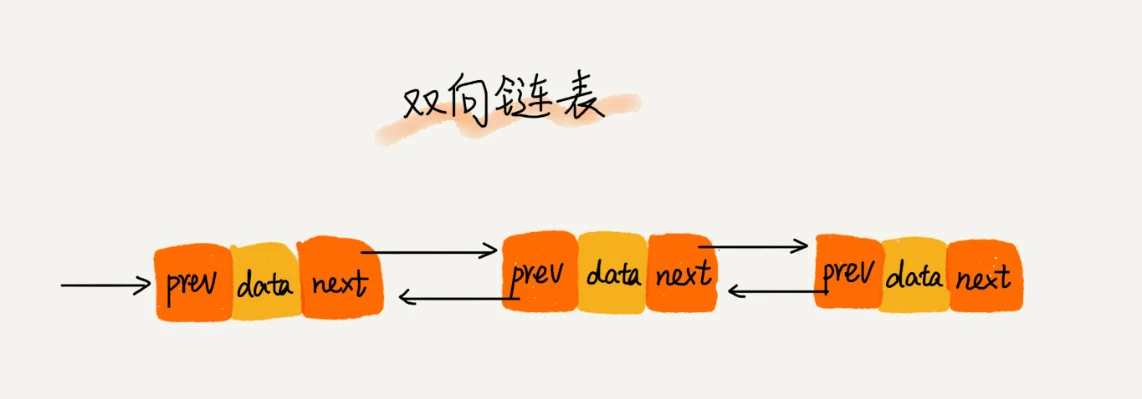

代码实现如下：

type LinkList struct {
	head *LinkNode
	tail *LinkNode
}

type LinkNode struct {
	data int
	next *LinkNode
	priv *LinkNode
}

func (l *LinkList) Insert(data int) {

	if l.head == nil {
		l.head = &LinkNode{
			data: data,
			next: nil,
			priv: nil,
		}
		l.tail = l.head
		return
	}
	t := l.head
	i := 0
	for t != nil {
		if i == 0 {
			if data < t.data {
				node := &LinkNode{
					data: data,
					next: t,
					priv: nil,
				}
				l.head.priv = node
				l.head = node
				return
			}
		}
		if data < t.data {
			node := &LinkNode{
				data: data,
				next: t,
				priv: t.priv,
			}
			t.priv.next = node
			t.priv = node
			return
		}
		t = t.next
		i++
	}
	node := &LinkNode{
		data: data,
		next: nil,
		priv: l.tail,
	}
	l.tail.next = node
	l.tail = node
}

func (l *LinkList) Print() {
	n := l.head
	for n != nil {
		fmt.Printf("n.data: %v\n", n.data)
		n = n.next
	}
}

func (l *LinkList) ReversePrint() {
	n := l.tail
	for n != nil {
		fmt.Printf("n.data: %v\n", n.data)
		n = n.priv
	}
}

循环链表

循环链表是单链表的一种变式，唯一的区别就是：尾节点的next不在指向null，而是指向头节点的地址。这样链表就变成了一个环形结构，它的优点就是从链尾到链头比较方便，适合处理具有环形结构特点的数据，比如约瑟夫环问题。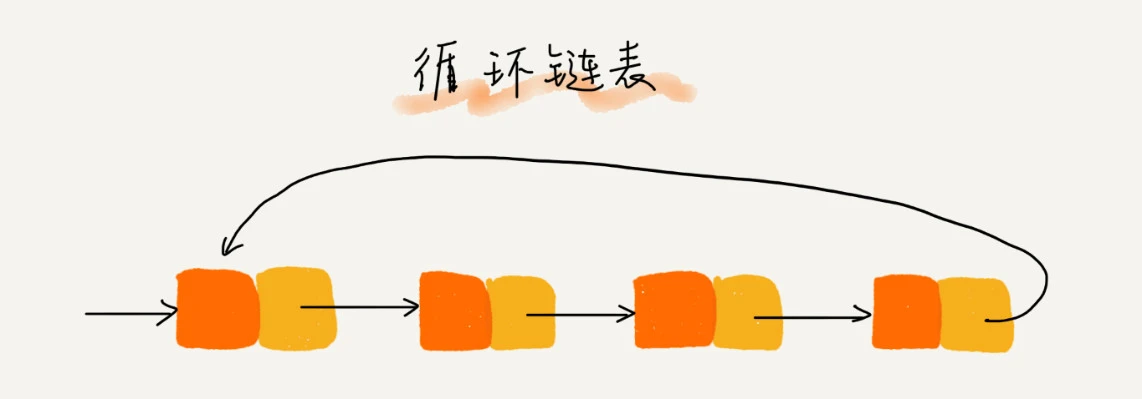

基于链表实现 LRU 缓存淘汰算法

思路是这样的：我们维护一个有序单链表，越靠近链表尾部的结点是越早之前访问的。当有一个新的数据被访问时，我们从链表头开始顺序遍历链表。

• 如果此数据之前已经被缓存在链表中了，我们遍历得到这个数据对应的结点，并将其从原来的位置删除，然后再插入到链表的头部。
• 如果此数据没有在缓存链表中，又可以分为两种情况：
  1. 如果此时缓存未满，则将此结点直接插入到链表的头部；
  2. 如果此时缓存已满，则链表尾结点删除，将新的数据结点插入链表的头部。

这样我们就用链表实现了一个 LRU 缓存，现在我们来看下缓存访问的时间复杂度是多少。因为不管缓存有没有满，我们都需要遍历一遍链表，所以这种基于链表的实现思路，缓存访问的时间复杂度为 O(n)。实际上，我们可以继续优化这个实现思路，比如引入散列表（Hash table）来记录每个数据的位置，将缓存访问的时间复杂度降到 O(1)。这部分的实现我计划在散列表中给出代码实现。

链表使用中的一些技巧

1. 函数中需要移动链表时，最好新建一个指针来移动，以免更改原始指针位置。
2. 链表中找环的思想：创建两个指针一个快指针一次走两步一个慢指针一次走一步，若相遇则有环，若先指向null指针则无环。
3. 链表中找中间节点思想：创建两个指针一个快指针一次走两步一个慢指针一次走一步，快指针到链尾时，慢指针刚好在中间节点位置。
4. 链表找倒数第k个节点思想：创建两个指针，第一个先走k-1步然后两个在一同走。第一个走到最后时则第二个指针指向倒数第k位置。
5. 反向链表思想：从前往后将每个节点的指针反向，即.next内的地址换成前一个节点的，但为了防止后面链表的丢失，在每次换之前需要先创建个指针指向下一个节点。